Python For GCSE
Turtle Graphics - Some Examples

Drawing A Clockface

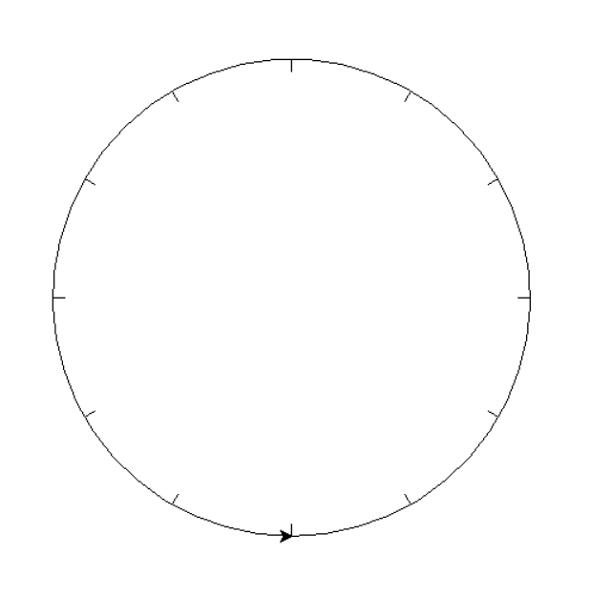
Turtle Program

import turtle as t

def draw_clock():
    t.delay(5)
    t.speed(10)
    for i in range(12):
        t.pu()
        t.goto(0,0)
        t.setheading(i*30+90)
        t.fd(190)
        t.pd()
        t.fd(10)        
    t.pu()
    t.goto(0,-200)
    t.setheading(0)
    t.pd()
    t.circle(200)
    
draw_clock()

Drawing Axes For A Graph

This program sets up some axes for a basic graph. With some extra code, you could plot a graph on top of this.

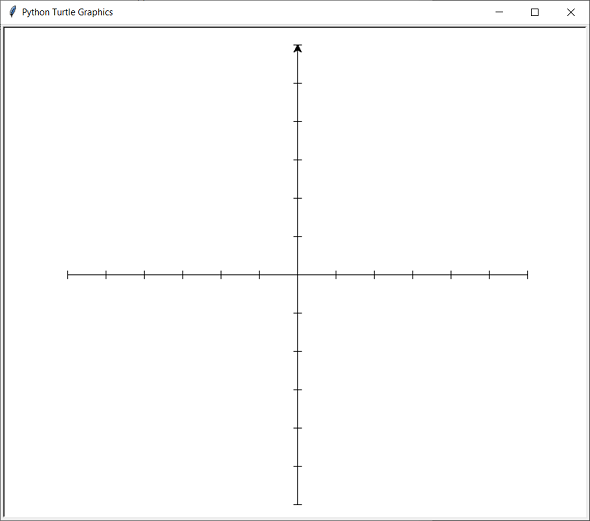
Turtle Program

import turtle as t

def draw_grid():
    t.pu()
    t.goto(-300,0)
    t.pd()
    # turn off animation
    t.delay(0)
    t.speed(0)
    # x axis
    t.setheading(0)
    for i in range(12):
        t.lt(90)
        t.fd(5)
        t.rt(180)
        t.fd(10)
        t.bk(5)
        t.setheading(0)
        t.fd(50)
    t.lt(90)
    t.fd(5)
    t.rt(180)
    t.fd(10)
    t.bk(5)
    t.pu()
    t.goto(0,-300)
    t.setheading(90)
    t.pd()
 
    # y axis
    for i in range(12):
        t.lt(90)
        t.fd(5)
        t.rt(180)
        t.fd(10)
        t.bk(5)
        t.setheading(90)
        t.fd(50)
    t.lt(90)
    t.fd(5)
    t.rt(180)
    t.fd(10)
    t.bk(5)
    t.setheading(90)

    
    # animate again
    t.speed(5)
    t.delay(5)

Sierpinski Triangle

There are several ways to construct the Sierpinski triangle. This method is called the Chaos Game. You start with an equilateral triangle. Draw a dot somewhere in the triangle. Choose one of the triangle's vertices at random. Draw a dot halfway from the current dot to that vertex. Repeat many times. The pattern shown below always emerges.

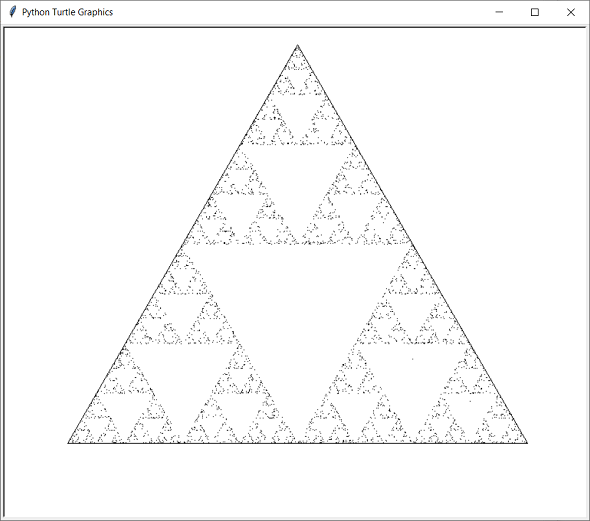
Turtle Program

import turtle as t
from random import choice

# starting point
t.pu()
t.lt(90)
t.fd(300)
t.pd()

# set up an equilateral triangle
v = []
v.append(t.pos())
t.rt(150)
t.fd(600)
v.append(t.pos())
t.rt(120)
t.fd(600)
v.append(t.pos())
t.goto(v[0])

t.pu()
t.home()

# turn animation off
t.speed(0)
t.delay(0)

t.ht()

# choose random vertex
# travel half distance
# draw dot
for i in range(10000):
    p = choice(v)
    # point at vertex at p
    t.seth(t.towards(p))
    # travel half distance
    t.fd(t.distance(p)/2)
    # dot
    t.dot(2, "black")