• Home
• Programming
• Computer Science
• Twisting Puzzles
• Arduino
• BBC micro:bit
• Raspberry Pi Pico

Computer Science

• Computer Science Home

Data Representation

• Binary Numbers
• Hexadecimal Numbers
• Character Coding Schemes
• Error Detection & Correction
• Bitmapped & Vector Graphics
• Image Compression Techniques
• Sound
• Real Numbers
• Logic Gates - Truth Tables
• Logic Gates - Diagrams
• Boolean Algebra

Program Design

• Principles Of Computation
• Problem Solving
• Hierarchy Charts
• Stepwise Refinement
• Finite State Machines
• State Transition Tables
• Decision Tables
• Algorithm Design
• Structured English
• Pseudocode
• Program Flowcharts
• Dry-Running
• Programming
• Structure Charts
• Structured Programming
• Testing
• Finite State Machines
• Turing Machines
• Types Of Problem
• The Systems Life Cycle

Hardware & Software

• Computer Architecture
• The Stored Program Concept
• Structure Of The Processor
• Machine Code Operations
• The Fetch-Execute Cycle
• Operating Systems
• Input Devices
• Output Devices
• Storage Devices
• Classification Of Software

Networks

• The Internet
• Domain Names & IP
• TCP/IP Protocol
• Web Design
• Communication Methods
• Networks
• Networks 2
• Server-Side Scripting
• Internet & Computer Security

Databases

• Entity Relationship Modelling
• Database Design
• Structured Query Language

Data Structures

• Stacks
• Queues
• Linear Lists
• Linked Lists
• Graphs
• Trees

Algorithms

• Recursion
• Binary Search
• Insertion Sort
• Hashing
• Simulations
• Comparing Algorithms

Other

• Computers & The Law
• Abstraction
• Regular Expressions
• Backus-Naur Form
• Reverse Polish Notation
• Programming Paradigms
• Object Oriented Programming

 

Computer Science
Finite State Machines

What Is A Finite State Machine?

If we start by simply interpreting the words that make up the name of the thing, we can say that a Finite State Machine is a machine that can be in only one of a fixed number of states at any time.

Think about a simple torch which has a single button for on and off. If the torch is off, pressing the button will turn it on. If it's on, pressing the button switches it off.

At the simplest level, the torch can therefore be said to have two states. It is an example of a finite state machine. The outcome of pressing the button depends on the state of the machine when the button is pressed.

Many types of digital machine are examples of FSMs. The computer you are probably using to view this page is one too. This is one of the reasons that you study this topic in Computing - because of the extent to which this concept relates to the architecture of the machines we call computers. It is also here because FSMs can be an important part of software development. There are plenty of tools (proprietary and open source) which allow you to represent FSMs visually using standard diagrams called State Transition Diagrams or Statecharts. You can also represent an FSM in a table called a State Transition Table. Using these tools, developers can work on abstract models of the software being developed. Many of these tools have provision for automatic code generation which allows designs to be implemented efficiently.

State Transition Diagrams

The torch described above can be represented using a State Transition Diagram like the one below.

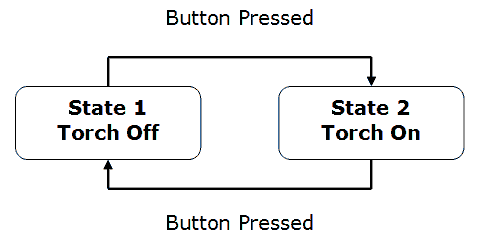
The boxes are the possible states for the machine. The arrows indicate a transition between two states. The pointer indicates the direction of the change. Each transition is labelled with the input that caused the transition to occur.

Another Example

Imagine a combination lock. It has a keypad with the digits 0 - 9. You need to enter the combination 1, 3 & 5 to unlock the treasure.

When we do a state transition diagram for this, we might do something like this,

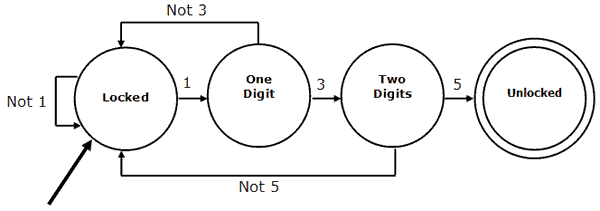
The arrow pointing into the locked state indicates the initial state. The double circle for the unlocked state indicates the goal or accepting state.

If you are struggling to follow the diagram, print it out and place your finger on the state marked locked. There are 2 arrows pointing out of this state. They are labelled 1 and not 1. Imagine that something other than a 1 is entered. This arrow points to the locked state - we're going nowhere. Now follow the arrow labelled 1, the correct first digit of the combination. This takes us to State 2, one digit has been correctly entered. From here the paths either take us to State 3, two digits correctly entered or, if we don't enter a 3, return to the initial state, locked. From State 3, we can reach the goal by entering a 5. At this point, we get the treasure.

The FSM above have no output. An FSM with no outputs is called a Finite State Automaton. FSAs have an initial state and at least one accepting state or goal.

Mealy Machines

When an FSM produces an output with each transition between states, it is known as a Mealy Machine. There is no accepting state. In a Mealy Machine, the output depends on both the previous state and the input.

Inputs and outputs are represented in state transition diagrams as you see below.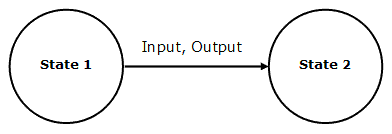

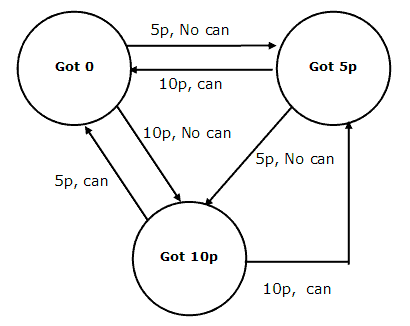
Vending Machine Example

Imagine a vending machine that sells cans of carbonated sugar water. This one isn't one of those machines that sells drinks made by those scummy international companies with their anti-union practices and hateful exploitation of the world's poorest people. As a result, it only costs 15p for each can of carbonated sugar water.

The machine accepts only 5p and 10p coinage. When 15p has been inserted into the machine, a can of carbonated sugar water is released.

Our Mealy Machine will have only 3 states. These are,

1. Got 0
2. Got 5p
3. Got 10p

When the machine has no money entered towards the cost of the can, it is in the state Got 0. Inserting coinage changes the state. Look carefully, this machine can cater for the different ways that you can arrive at 15p using the two coins. If two 10p coins are inserted, a can is released and the machine moves to the Got 5 state. An extension to this machine might be to cater for the release of change after or before the purchase is completed.